§ 1. Общие сведения
1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму.
Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин.
Широкое использование конических соединений объясняется рядом их преимуществ.
1. Они обеспечивают высокую точность центрирования деталей.
2. При плотном соприкосновении пологих конусов получается неподвижное соединение.
3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними.
2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а).
Точка пересечения образующей с осью называется вершиной конуса.
Плоскости, перпендикулярные к оси конуса, называются, основаниями.
Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим).
Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими.
Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон.
Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле
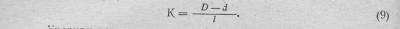
Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле
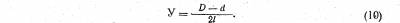
Из формул (9) и (10) видно, что уклон равен половине конусности.
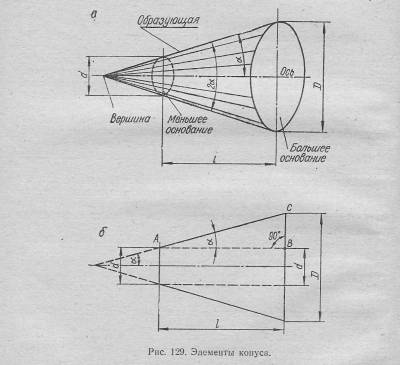
Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е.
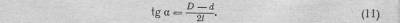
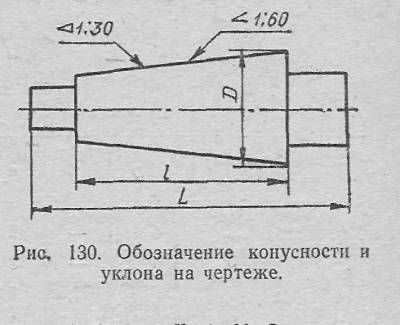
На чертеже (рис. 130) конусность обозначают знаком <, а уклон —, острие которых направляется в сторону вершины конуса. После знака указывается отношение двух цифр. Первая из них соответствует разности диаметров в двух принятых сечениях конуса, вторая для конусности— расстояние между сечениями, для уклона — удвоенной величине этого расстояния.
Конусность и уклон иногда записываются числами десятичной дроби: 6,02; 0,04; 0,1 и т. д. Для конусности эти цифры соответствуют разности диаметров конуса на длине 1 мм, для уклона — разности радиусов на этой же длине.
Для обработки полного конуса достаточно знать два элемента: диаметр основания и длину; для усеченного конуса — три элемента: диаметры большего и меньшего оснований и длину. Вместо одного из указанных элементов может быть задан угол наклона а, уклон или конусность. В этом случае для определения недостающих размеров пользуются вышеприведенными формулами (9), (10) и (11).
Пример 1. Дан конус, у которого d=30 мм, /=500 мм, К=1: 20. Определить больший диаметр конуса.
Решение. Из формулы (9)

Пример 2. Дан конус, у которого D=40 мм, l = 100 мм, а=5 , Определить меньший диаметр конуса.
Решение. Из формулы (11)
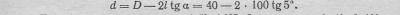
По таблице тангенсов находим tg5°=0,087. Следовательно, d=40—2*100Х Х0,87=22,6 мм.
Пример 3. Определить угол уклона а, если на чертеже указаны размеры конуса: D—50 мм, d=30 мм, /=200 мм.
Решение. По формуле (11)

Из таблицы тангенсов находим а=2 50 .
Пример 4. Дан конус, у которого D=60 мм, /=150 мм, К=1 : 50. Определить угол уклона а.
Решение. Так как уклон равен половине конусности, можно записать:

По таблице тангенсов находим а=0 30 .
3. Нормальные конусы. Конусы, размеры которых стандартизованы, называются нормальными. К ним относятся конусы Морзе, метрические, конусы для насадных разверток и зенкеров с конусностью 1:50 0, под конические штифты — с конусностью 1:50, для конических резьб с конусностью 1 : 16 и др.
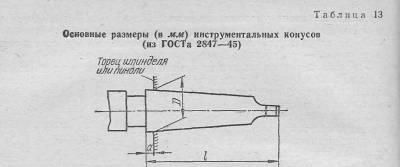
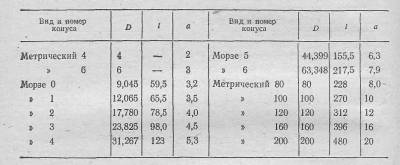
Наибольшее распространение в машиностроении получили инструментальные конусы Морзе и метрические, основные размеры которых приведены в табл. 13.
1. Область применения конусов. Наряду с цилиндрическими деталями в машиностроении получили довольно широкое распространение детали с коническими поверхностями. Примерами их могут служить конусы центров, хвостовиков сверл, зенкеров, разверток. Для крепления этих инструментов передние участки отверстий шпинделя и пиноли токарного станка имеют также коническую форму.
Однако область использования конусов не ограничивается режущими инструментами. Конические поверхности имеют многие детали машин.
Широкое использование конических соединений объясняется рядом их преимуществ.
1. Они обеспечивают высокую точность центрирования деталей.
2. При плотном соприкосновении пологих конусов получается неподвижное соединение.
3. Изменяя осевое положение деталей конического соединения, можно регулировать величину зазора между ними.
2. Конус и его элементы. Конус представляет собой геометрическое тело, поверхность которого получается вращением прямой линии (образующей), наклонно расположенной к оси вращения (рис. 129, а).
Точка пересечения образующей с осью называется вершиной конуса.
Плоскости, перпендикулярные к оси конуса, называются, основаниями.
Различают полный и усеченный конусы. Первый расположен между основанием и вершиной, второй — между двумя основаниями (большим и меньшим).
Конус характеризуется следующими элементами: диаметром большего основания D; диаметром меньшего основания d; длиной l; углом уклона а между образующей и осью конуса; углом конуса 2а между противоположными образующими.
Кроме этого, на рабочих чертежах конических деталей часто употребляют понятия конусность и уклон.
Конусностью называется отношение разности диаметров двух перечных сечений конуса к расстоянию между ними. Она опреляется по формуле
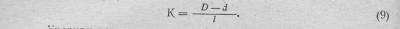
Уклоном называется отношение разности радиусов двух поперечных сечений конуса к расстоянию между ними. Его определяют по формуле
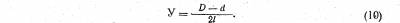
Из формул (9) и (10) видно, что уклон равен половине конусности.

Тригонометрически уклон равен тангенсу угла уклона (см. рис. 129, б, треугольник ABC), т. е.
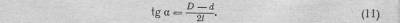
На чертеже (рис. 130) конусность обозначают знаком <, а уклон —, острие которых направляется в сторону вершины конуса. После знака указывается отношение двух цифр. Первая из них соответствует разности диаметров в двух принятых сечениях конуса, вторая для конусности— расстояние между сечениями, для уклона — удвоенной величине этого расстояния.
Конусность и уклон иногда записываются числами десятичной дроби: 6,02; 0,04; 0,1 и т. д. Для конусности эти цифры соответствуют разности диаметров конуса на длине 1 мм, для уклона — разности радиусов на этой же длине.
Для обработки полного конуса достаточно знать два элемента: диаметр основания и длину; для усеченного конуса — три элемента: диаметры большего и меньшего оснований и длину. Вместо одного из указанных элементов может быть задан угол наклона а, уклон или конусность. В этом случае для определения недостающих размеров пользуются вышеприведенными формулами (9), (10) и (11).

Пример 1. Дан конус, у которого d=30 мм, /=500 мм, К=1: 20. Определить больший диаметр конуса.
Решение. Из формулы (9)

Пример 2. Дан конус, у которого D=40 мм, l = 100 мм, а=5 , Определить меньший диаметр конуса.
Решение. Из формулы (11)
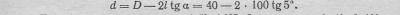
По таблице тангенсов находим tg5°=0,087. Следовательно, d=40—2*100Х Х0,87=22,6 мм.
Пример 3. Определить угол уклона а, если на чертеже указаны размеры конуса: D—50 мм, d=30 мм, /=200 мм.
Решение. По формуле (11)

Из таблицы тангенсов находим а=2 50 .
Пример 4. Дан конус, у которого D=60 мм, /=150 мм, К=1 : 50. Определить угол уклона а.
Решение. Так как уклон равен половине конусности, можно записать:

По таблице тангенсов находим а=0 30 .
3. Нормальные конусы. Конусы, размеры которых стандартизованы, называются нормальными. К ним относятся конусы Морзе, метрические, конусы для насадных разверток и зенкеров с конусностью 1:50 0, под конические штифты — с конусностью 1:50, для конических резьб с конусностью 1 : 16 и др.
Наибольшее распространение в машиностроении получили инструментальные конусы Морзе и метрические, основные размеры которых приведены в табл. 13.

Размеры конусов Морзе выражаются дробными числами. Это объясняется тем, что впервые стандарт на них был принят в дюймовой системе измерения, которая сохранилась до настоящего времени. Конусы Морзе имеют различную конусность (примерно 1 20), метрические конусы одинаковую — 1:20.
Автор - nastia19071991
- Войдите, чтобы оставлять комментарии